Collaptz

The Collatz conjecture is one of the most famous unsolved problems in mathematics. It has been around for over 90 years and is one of those problems that, at a first glance is simple and intuitive, yet incredibly hard to be proven. Concretely, a Collatz sequence begins with a positive integer and follows two simple rules: if the current number is even, it is divided by two; if it is odd, it's tripled and increased by one. The Collatz conjecture proposes that for any natural number such sequence will inevitably reach one. For example, taking number 12 as an input we get a sequence of 12 -> 6 -> 3 -> 10 -> 5 -> 16 -> 8 -> 4 -> 2 -> 1.

Even though there is no analytical prove for the conjecture, we can obtain fascinating empirical data about the behaviour of these sequences such as distributions of their lengths (stopping times). However, as the sequences' initial values approach infinity, it becomes infeasible to perform this computation on a single machine, so the natural way of parallelizing such task is to perform it in a distributed way, i.e. on cluster of computers. But how can we ensure that the computation is done in the correct way and the resulting sequence was really produced by the same program? That is where the zkVM comes into play! We can obtain a "receipt" of computational integrity by running this partial the computation in a zkVM, which allows to trustlessly distribute the computation, thereby enabling contributions from public/untrusted participants.

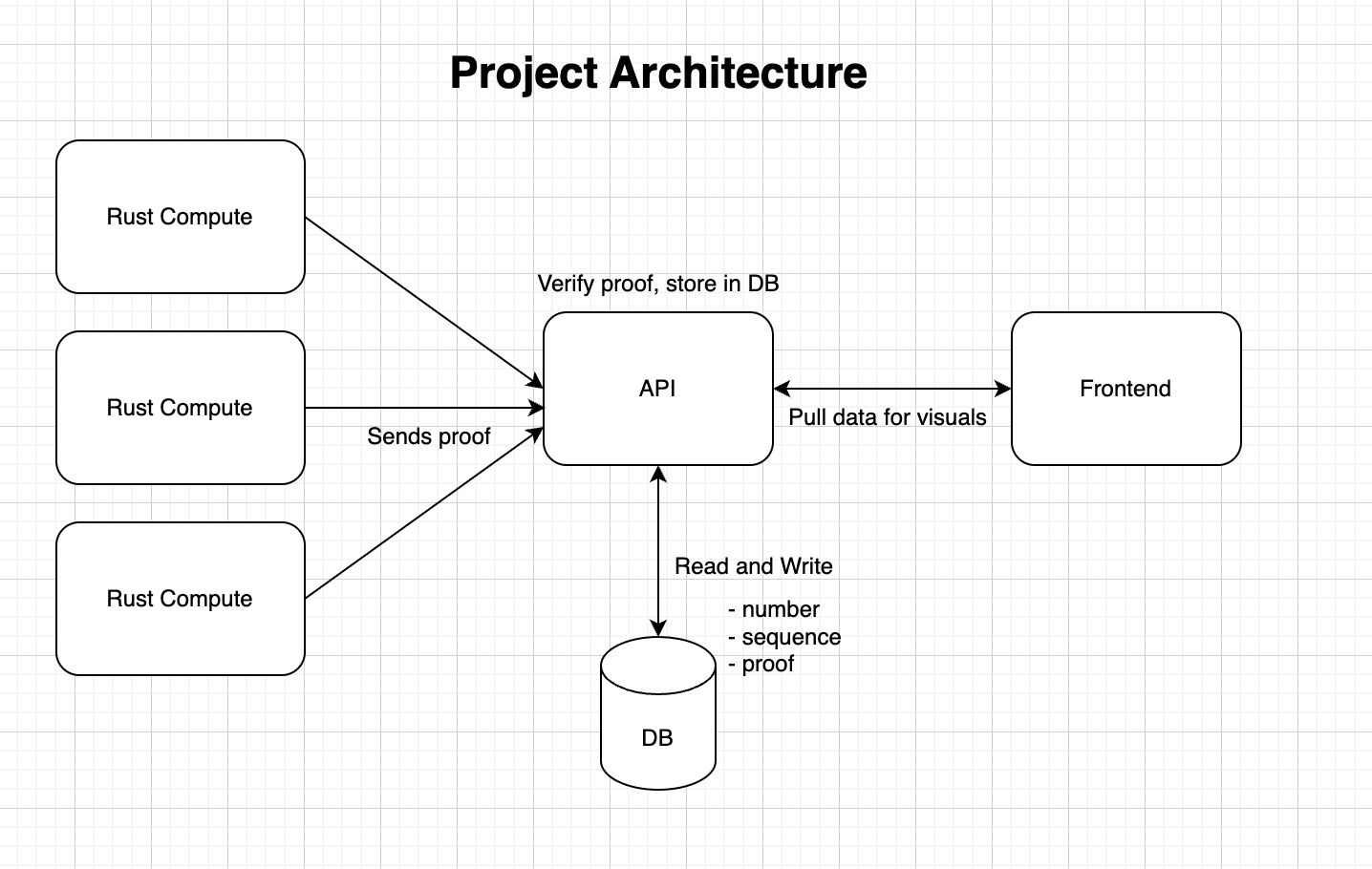
Collaptz is made of 3 components:

1. Trustless compute: computes Collatz sequences and provide proofs for a computation and pushes the results to a public database.
2. Storage layer: Verifies the computational results from the compute nodes, writing only valid ones.
3. Dashboard: Visualizes the Collatz dataset.

The main technology used is risc0's zkVM. It creates and verifies "receipts" or proofs of computation. These receipts are sent to a python HTTP server which uses risc0 to verify the receipt. If the receipt is valid then the receipt and its output (the Collatz sequence) are written to the database. The collected results are visualized through a web client.